数字集成电路笔记

发表于 更新于 本文字数： 2.4k 阅读时长 ≈ 2 分钟

数字集成电路笔记

面经

数字分频器

  1. 笔记链接
  2. 作用：将高频信号分频为低频信号；配合DSP使用可以得到高频信号
  3. 偶数分频:
    • 方法1：通过寄存器延时获得2,4,8,...,等分频
    • 方法2：通过计数器实现分频；如果需要实现6分频，则需要一个计数器，从0开始计数，到2的时候，将目标信号进行翻转即可
  4. 奇数分频:
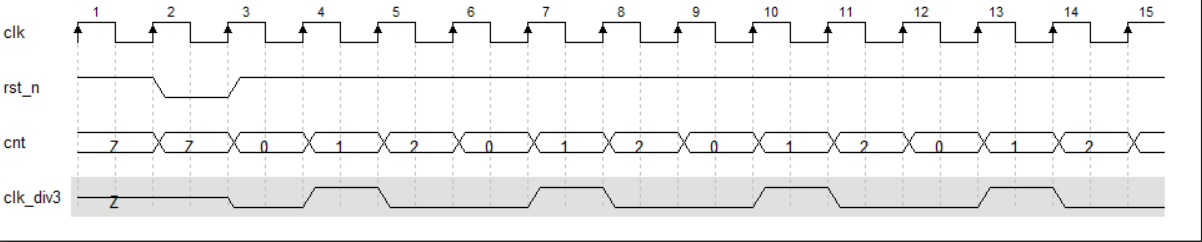
    • （高低占比不是各50%）: 计数器为0、(n-1)/2的时候，都将目标信号翻转即可，例如下图3分频，计数器为0，2的时候，翻转即可
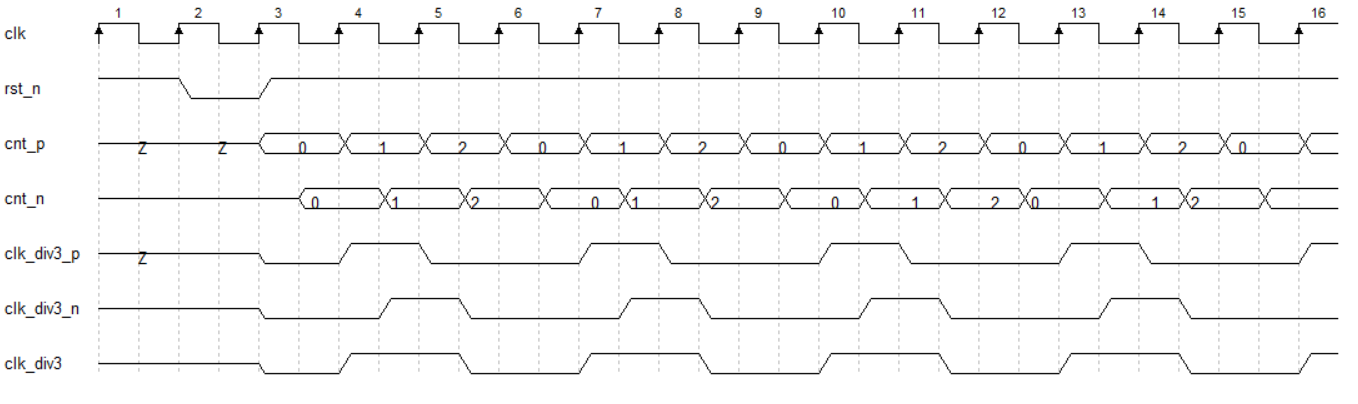
    • （高低占比是各50%）:需要2个计数器，分别在上升沿跟下降沿+1，这两个计数器到达n-1时，信号翻转；将得到的两个信号进行或操作

边沿检测

  1. 作用：检测信号的上升沿、下降沿
  2. 实现: din_r是din延迟1拍的信号 
    1
    2
    3
    assign up_edge   = ~din_r & din;
    assign down_edge = din_r & ~din;
    assign both_edge = din_r ^ din;

CDC(Clock Domain Crossing)问题

单bit信号快到慢

  1. 通过握手信号&延长快时钟域信号展宽来保证慢时钟域可以采样到快时钟域的信号:

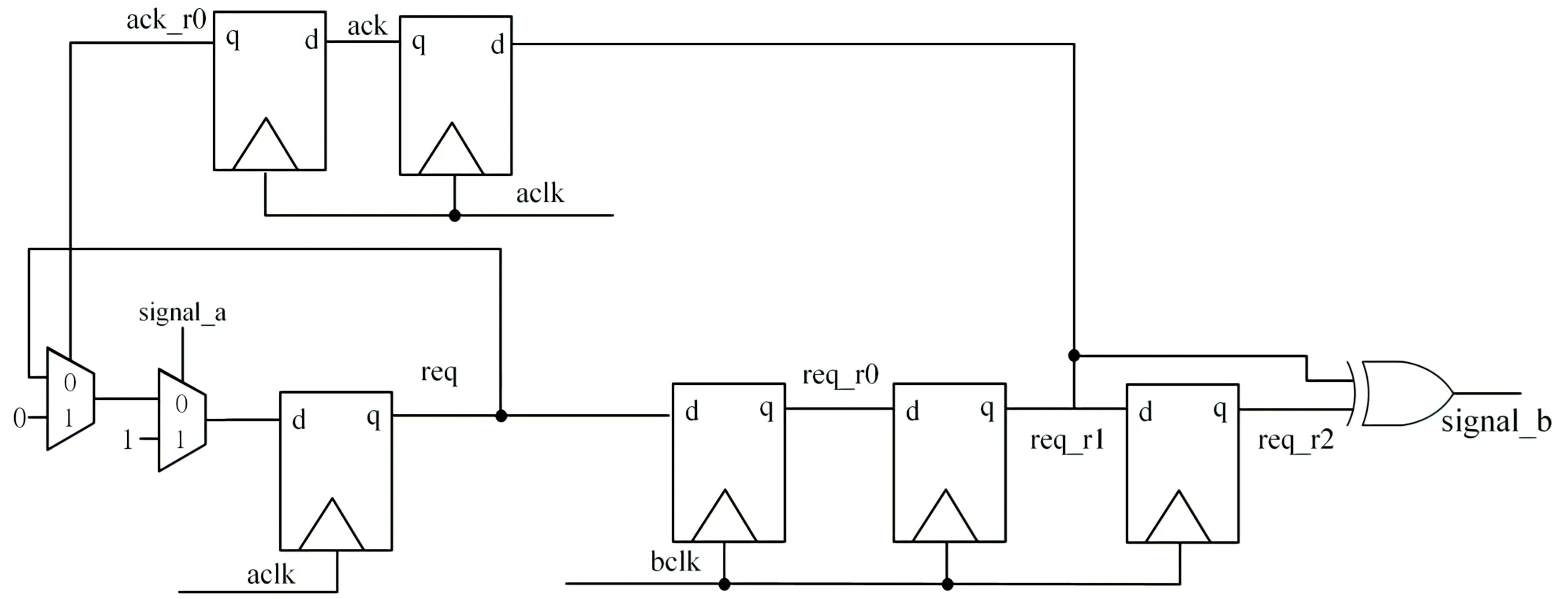
    • 快时钟域对脉冲信号进行检测，检测为高电平时输出高电平信号req。

    • 慢时钟域对快时钟域的信号req进行延迟打拍采样。因为此时的脉冲信号被快时钟域保持拉高状态， 延迟打拍肯定会采集到该信号。

    • 慢时钟域确认采样得到高电平信号req_r2后，拉高反馈信号ack再反馈给快时钟域。

    • 快时钟域对反馈信号ack进行延迟打拍采样得到ack_r0。如果检测到反馈信号为高电平， 证明慢时钟域已经接收到有效的高电平信号，信号恢复原来状态

FIFO 问题

STA(Static Timing Analysis)

contamination delay(\(T_{cd}\)) & propagation delay(\(T_{pd}\))

假设有一个buffer，其输入为A，输出为Y

  • \(T_{cd}\): A开始变化到Y开始变化的时间
  • \(T_{pd}\): A开始变化到Y变化到最终稳定的时间

Hazard & Glitch

  • Hazard：电路的特性，在组合电路中，各个输入端变化不是严格同步的，导致输出可能会存在亚稳态
  • Glitch：Hazard导致的输出Y出现的波动，由于输入不是同时到达组合电路的，因此组合电路的输出可能会有瞬时变化

Sequential logic delays

假设寄存器的输入为D，输出为Q

  • \(T_{setup}\), \(T_{hold}\): D需要在clk上升沿到达之前\(T_{setup}\)保持稳定，在clk上升沿之后\(T_{hold}\)保持稳定，否则Q会进入亚稳态(metastability)
  • \(T_{cq}\): 又叫做clock to output dealy, 时钟clk上升沿一半的时刻到Q变化到一半的时刻（clk上升沿到Q开始变化的时刻）
  • \(T_{setup}\), \(T_{hold}\), \(T_{cq}\)都可以在寄存器的说明书(datasheet)里找到

Timing

假设寄存器的输入为D，输出为Q，有寄存器A到寄存器B的数据通路

Setup Time

  1. 定义：在clock的上升沿前setup时间，D必须保持稳定不在变化，否则寄存器的输出Q会处于不稳定态(metastability)

  2. 什么时候会违反Setup Time 约束(setup violation): 本质原因是数据从A到达B太迟了， 导致B寄存器要求的\(D_B\)应该稳定的时刻，数据还在发生变化

    • 时钟周期T太短
    • 寄存器之间的组合逻辑太长，传播时延太大
    • 假设\(T_{skew}>0\)，即B的clock由于线路延时比A的clock后到达，则\(T_{skew}\)的存在让Hold Time更容易满足

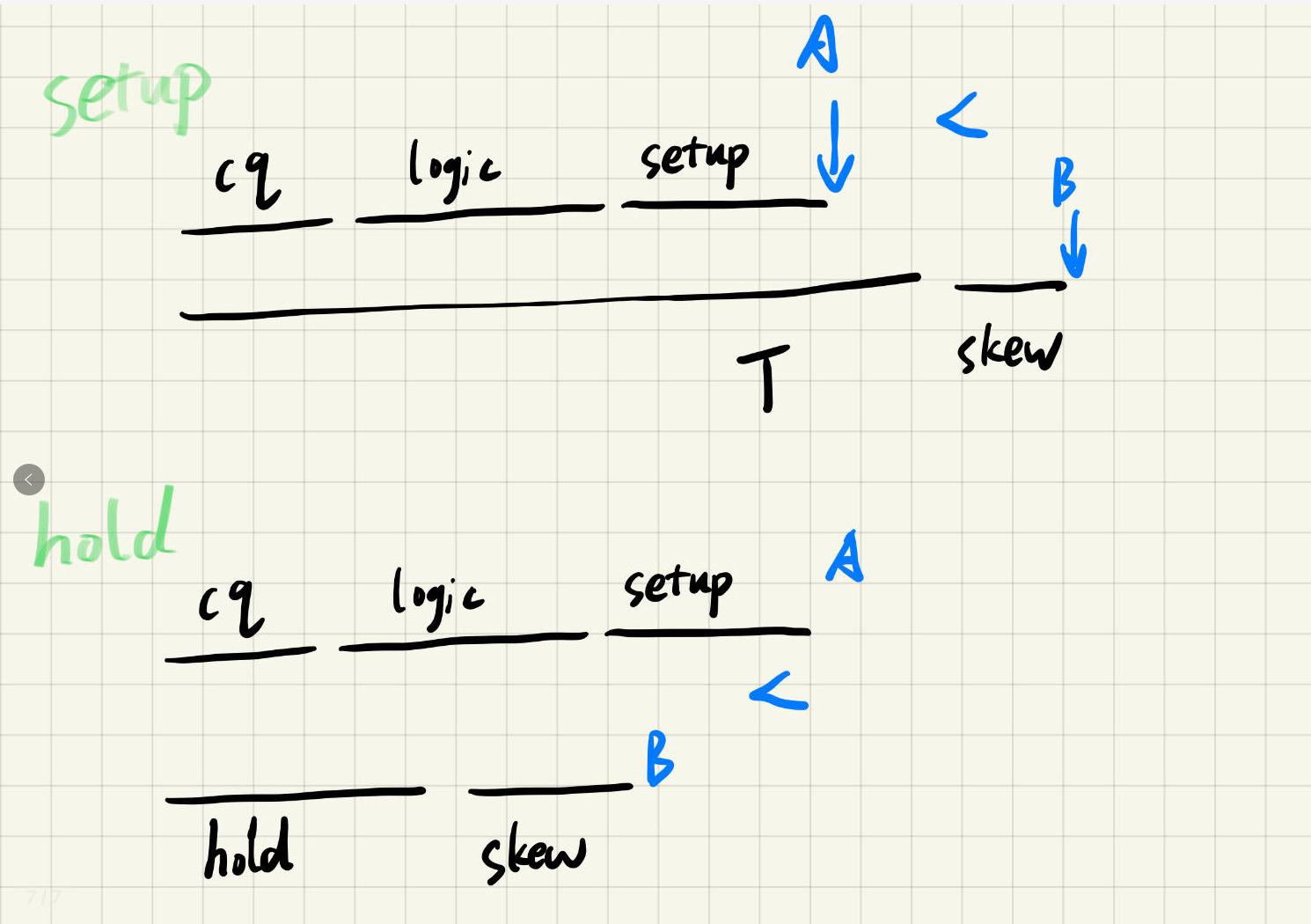
    \(T_{cq\_A}+T_{logic}+T_{setup} < T+T_{skew}\)，不考虑\(T_{cq}, T_{skew} \rightarrow T_{logic}<T-T{setup}\)

    • \(T_{cq\_A}\): 寄存器A时钟上升沿到\(Q_A\)开始变化的时间

Hold Time

  1. 定义：在clock的上升沿后hold时间，D必须保持稳定不变

  2. 违反Hold Time约束的原因：A->B的第二笔数据太快到达B了，导致上一个cycle的数据被冲刷掉:

    • 寄存器之间组合逻辑太短，时延太短
    • 假设\(T_{skew}>0\)，即B的clock由于线路延时比A的clock后到达，则\(T_{skew}\)的存在让Hold Time更难满足

    \(T_{cq\_A}+T_{logic}<T_{hold}+T_{skew}\)，不考虑\(T_{cq}, T_{skew} \rightarrow T_{logic}>T_{hold}\)

    PS: 考虑\(T_{hold}\)的时候，没有考虑周期T，因为是第二笔数据到达太块，第二笔数据跟B采样的时候，是同一个周期

  3. 总结：时序上应该满足\(T_{hold} < T_{logic} < T-T_{setup} , T_{setup}+T_{hold}<T\)

如何计算最大频率

  1. \(f=1/T\), 找到满足时序约束的最小的T即可
  2. 如上所述，T跟\(T_{hold}\)没有关系，只跟\(T_{setup}\)有关系:
    \(T>T_{logic}+T_{setup}-T_{skew}\rightarrow f<1/T=1/(T_{logic}+T_{setup}-T_{skew})\)

Latch to FF(Flip Flop)

  1. 结构
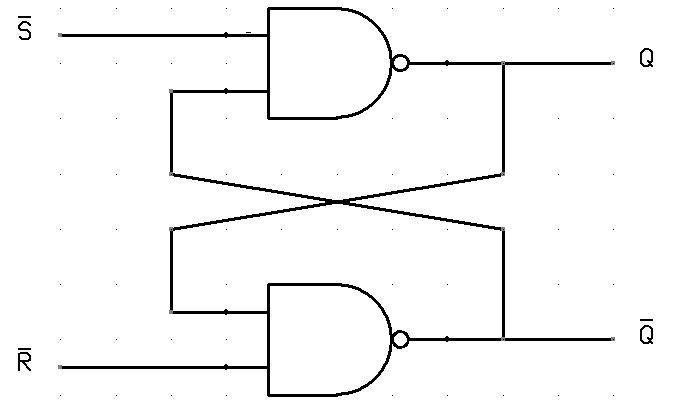
    • Latch(PS: Latch 其实有多种实现结构)
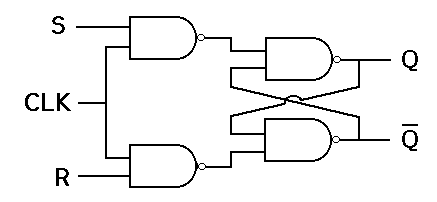
    • FF

TODO: use K-Map to reduce Glitch

参考资料:

Name

  1. 笔记链接

体系结构

参考资料

面经

  1. 数字IC经典电路设计

体系结构